The main evidence for the existence of dark matter is the flat rotation curve of galaxies, and high peculiar velocities of galaxies in galaxy clusters.
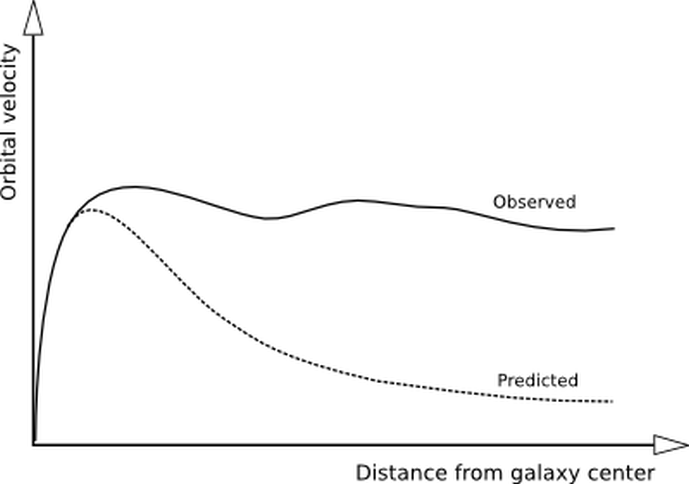
The mass eclosed in a radius R is derived from the Keplerian equation M[SUB](R)[/SUB] = v2R/G .
Also we know about the existence of gravitational lensing.
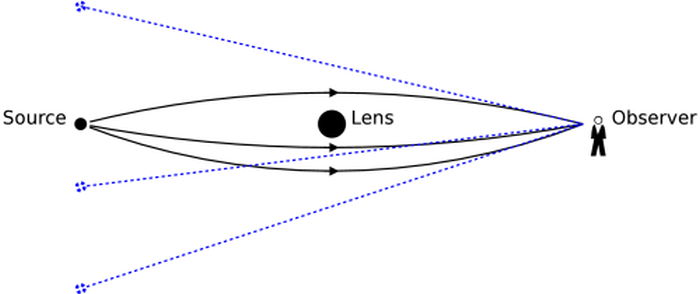
My question is this: was gravitational lensing taken into account when galactic rotation curves were plotted? Because here is an effect of gravitational lensing that I didn`t find mention of:

The photon emmited by the star can`t travel directly to the observer because it is gravitationally pulled to the center of the galaxy, so its trajectory is bent. And because of this bending effect the observer will see the star as being farther away from the galactic center. This in turn will push the observer to the conclusion that there is more mass enclosed in the observed radius. If the orbital speed of the star is not calculated from it’s red shift then it will also appear to be bigger then it actually is, since v = w*r, where w – angular velocity, r – observed radius.
Consequences:
1) All massive celestial objects appear greater then they actually are.
2) The farther away the celestial object from the observer the stronger the magnification effect.

3) Most of the distant celestial object that we observe are not actually in the direction that we observe them.

P.S.: The fish is also distorted


The mass eclosed in a radius R is derived from the Keplerian equation M[SUB](R)[/SUB] = v2R/G .
Also we know about the existence of gravitational lensing.

My question is this: was gravitational lensing taken into account when galactic rotation curves were plotted? Because here is an effect of gravitational lensing that I didn`t find mention of:

The photon emmited by the star can`t travel directly to the observer because it is gravitationally pulled to the center of the galaxy, so its trajectory is bent. And because of this bending effect the observer will see the star as being farther away from the galactic center. This in turn will push the observer to the conclusion that there is more mass enclosed in the observed radius. If the orbital speed of the star is not calculated from it’s red shift then it will also appear to be bigger then it actually is, since v = w*r, where w – angular velocity, r – observed radius.
Consequences:
1) All massive celestial objects appear greater then they actually are.
2) The farther away the celestial object from the observer the stronger the magnification effect.

3) Most of the distant celestial object that we observe are not actually in the direction that we observe them.

P.S.: The fish is also distorted

