Long Distance Supercruise times - Anyone got rough numbers?
- Thread starter mossfoot
- Start date
I collected quite a few distance/times and used Excel to experiment with trend lines and reveal its magic formula when the line looked "right". The best fit I got was using a 3 term polynomial trend line. Let me state now, I am no mathematician, but I know Excel quite well. I can reason subjectively that the 3 term polynomial curve is good because there is slow initial acceleration, then steady acceleration up to a maximum (2001) after which speed is constant. I'm sure there are maths boffins out there who can comment on that
Here is the curve...View attachment 65587
(snip)
I love this approach but I think you need to try to fit to a different function. Your curve suggests that you somehow slow down when your trip is longer, and we all know that isn't true. If you look at the last three points you'll see they lie on a straight line. That makes sense: your distance traveled becomes more linear as you spend more and more time near top speed. I would suggest something that approaches a straight line in the limit. One example would be a hyperbola, but because your slowest possible speed isn't zero, you'd need some kind of offset.
So it would be really interesting if you could try fitting to something like
time = b² * (√(1 + (distance+c)²/a²) - √(1 + c²/a²))
Because it's a hyperbola, the slope should reach b²/a² in the limit (if I recall correctly). The second √ term is there so time = 0 when distance = 0.
I think that this is right.
I am using:
A*sqrt(d*d - 1)+B
where A = 38.81, B=1.242 and d = [Distance]/[6e6 ls]+1.0
To give the travel time in minutes.
Here is a plot of this curve (edit - transparency hides the axis labels on black background!)
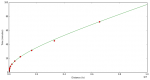
The red points are simulations based on my understanding of the travel mechanic. It comes out like:
speed = 2000*c*math.sqrt(min(distance,traveled)/(1e6*u.ls))
speed = min(max(30*u.km/u.s,speed),maxspeed)
and once the time to arrival is less than 7 seconds, we just hold the time to arrival at 7 until we get to 1Mm.
Last edited:
I don't really keep track of the numbers but this is how I usually do it :
50,000LS = visit bathroom and get a drink, maybe a small snack.
100,000LS = Enough to wash your car inside and out.
200,000LS = Enough to go buy groceries, don't worry you'll be back in time for a few more minutes of staring at supercruise.
50,000LS = visit bathroom and get a drink, maybe a small snack.
100,000LS = Enough to wash your car inside and out.
200,000LS = Enough to go buy groceries, don't worry you'll be back in time for a few more minutes of staring at supercruise.
Han did the Hutton run in under 12 minutes.
That's the ship decelerating due to the target coming closer, try that and deselect the station, shouldn't happen anymore then as it doesn't have a gravity well.
I always had the impression that it starts getting slower past 1800c or somewhere around.
Still, all this makes me want the answer to one question: What does FD expect us to do on these eventless straight line screensaver travels? Like really, what'd they think this would add gameplay wise?
Please someone enlighten me because I always end up with "they hate us and want us to hate SC" : / that's what I feel every time I go somewhere that's more than 10k Ls away, nothing but staring at the ETA go down, then it almost stops going down because I started to decelerate.
Can someone really honestly say they enjoy these times of "nothing to do, just staring at dots zipping by"? Well aside of the FD devs
Sidenote, I came here because I had to cover 32k Ls and had nothing to do while waiting.
2nd sidenote, forgot I had to go back the 32k Ls because I was smuggling and wanted to risk less bounty should I screw up so unloaded the other portion first, and if jumping to a nearby system and jumping back being faster than SC'ing back then I have no idea IF there's any good example of how too-long SC times are.
Last edited: