Kepler & Galileo
Galileo, born approximately 100 years after Copernicus, revolutionized astronomy with the use of the telescope. He was able to observe the phases of Venus, which is an inner planet that will never show us its fully illuminated side, which proved the heliocentric model. He also observed moons circling Jupiter.
Around the same time, Johannes Kepler was working out a series of laws to describe the orbits of the planets around the sun. It took him about 10 years to complete his book,
Astronomia Nova (A New Astronomy), before publishing it. In his book, he outlined equations and terminology to fully describe elliptical orbits in three dimensions, all of which are still in use today.
Prior to working out his theory, Kepler had worked as an assistant to the astronomer Tycho Brahe, who had collected a lifetime of astronomical observations, but kept it mostly hidden from Kepler for fear that he would use it to try to prove a Copernican heliocentric theory. When Tycho Brahe died, the collection of data passed on to Kepler, who was able to use it for completing his theory.
Like those who came before him, Kepler believed that orbits should be perfect circles, but struggled to make that work with the recorded observations of Mars that Brahe had collected. Eventually he stumbled upon the fact that an imaginary line drawn from the Sun to a planet's position will sweep out an equal area of space in an equal time, regardless of which side of the orbit the planet is in, and how fast it is moving there.
This discovery, which became his second law of orbital motion, led to what became his first law: that the planets move in elliptical orbits, with the sun at one focus of the ellipse. His third law shows that there is a precise relationship between the planet's distance from the sun, and the period of the orbit (the length of time it takes to complete one orbit).
Kepler had tried various other orbital shapes, including an egg-shaped ovoid, to explain the equal area over equal time phenomenon. This was unsuccessful until after approximately 40 attempts, that he tried fitting it to an ellipse. He had previously dismissed it as too simple of a solution to have been overlooked by his predecessors. Once he demonstrated that this perfectly fit the Mars data, he concluded that it must be true for all of the planets.
What Kepler lacked though, was an understanding of
why. He proposed that there were two forces acting upon the planets: one to propel them forward through their paths, and one to attract them toward the sun. What he didn't understand was that these were simply inertia and gravity, respectively. He did however correctly deduce that whatever solar force was acting on the planets, it must lose strength over distance, since the planets move more slowly when they're further away.
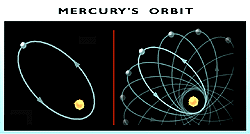
While very precise, there are still orbital effects that can't be accounted for using his perfect elliptical equations. His system assumes a
2-body system, with planets represented as point-masses orbiting a stationary sun. In reality, the sun orbits a barycenter that is contained within itself, and the planets interact with each other in subtle ways. This is referred to as the
N-body problem, and it results in the orbits changing over time, in many cases oscillating in eccentricity, and perhaps also a precession of the orbit, meaning the direction of the ellipse's long axis can slowly rotate. Newtons laws of motion and universal gravitation were still decades away.
(As an aside, my ship is named
Astronomia Nova, after Kepler's book)
EDIT: Aside #2: Elite uses perfect Kepler orbits in the game.