This is a followup to my previous post, which was about lattices in 3-dimensional Euclidean space, used as alien artifacts. This one is about "lattices" in 3-dimensional spherical space (sometimes called the 3-sphere), which is the unit sphere in 4-dimensional Euclidean space. A 3-dimensional polyhedron can be drawn like a beach ball on the surface of an ordinary sphere (mathematicians call this the 2-sphere) in 3D space, which gives a "lattice-like" structure on the sphere. Similarly, 4D polytopes (the analogues of the 3-dimensional polyhedra) give a lattice-like structure on the 3-sphere. Then we can draw these things back in 3-dimensional Euclidean space using something called stereographic projection.
Ok anyway, enough theory, what do these look like?
WebGL rotatable model.
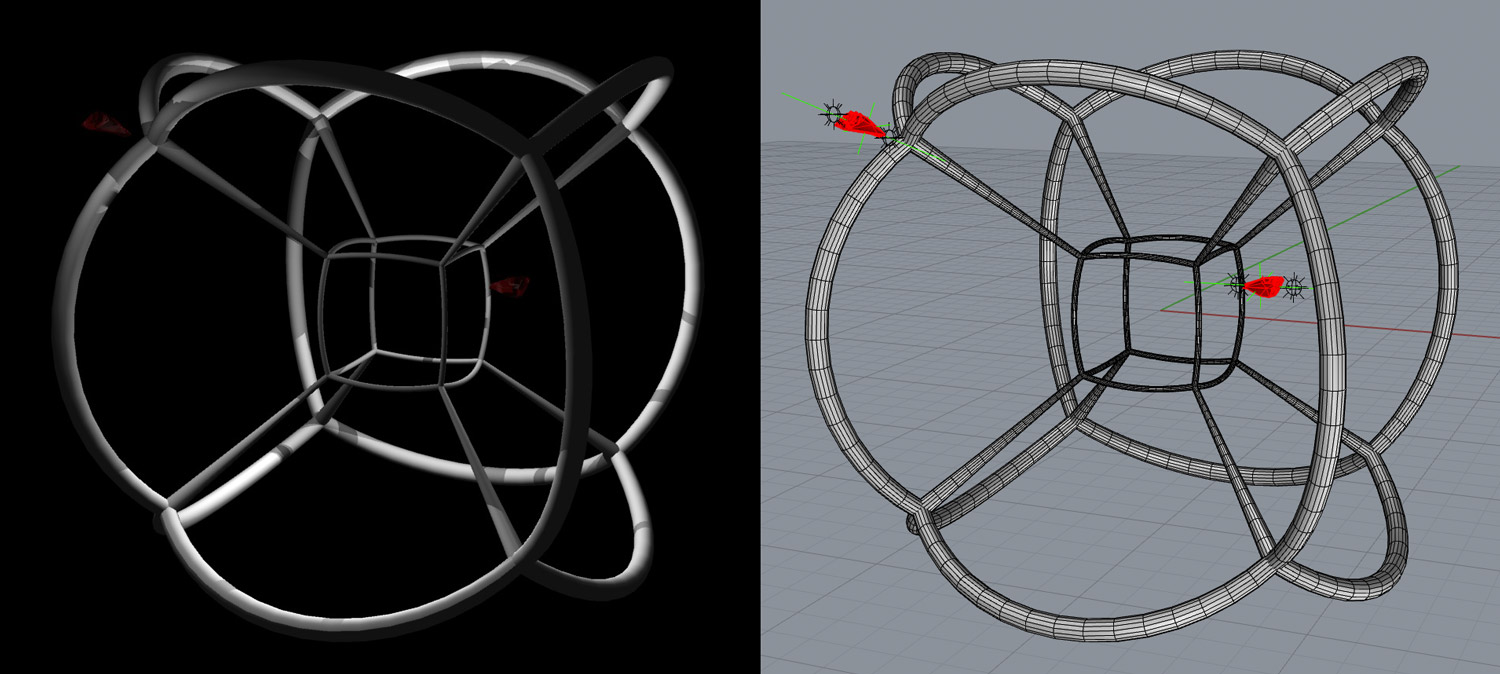
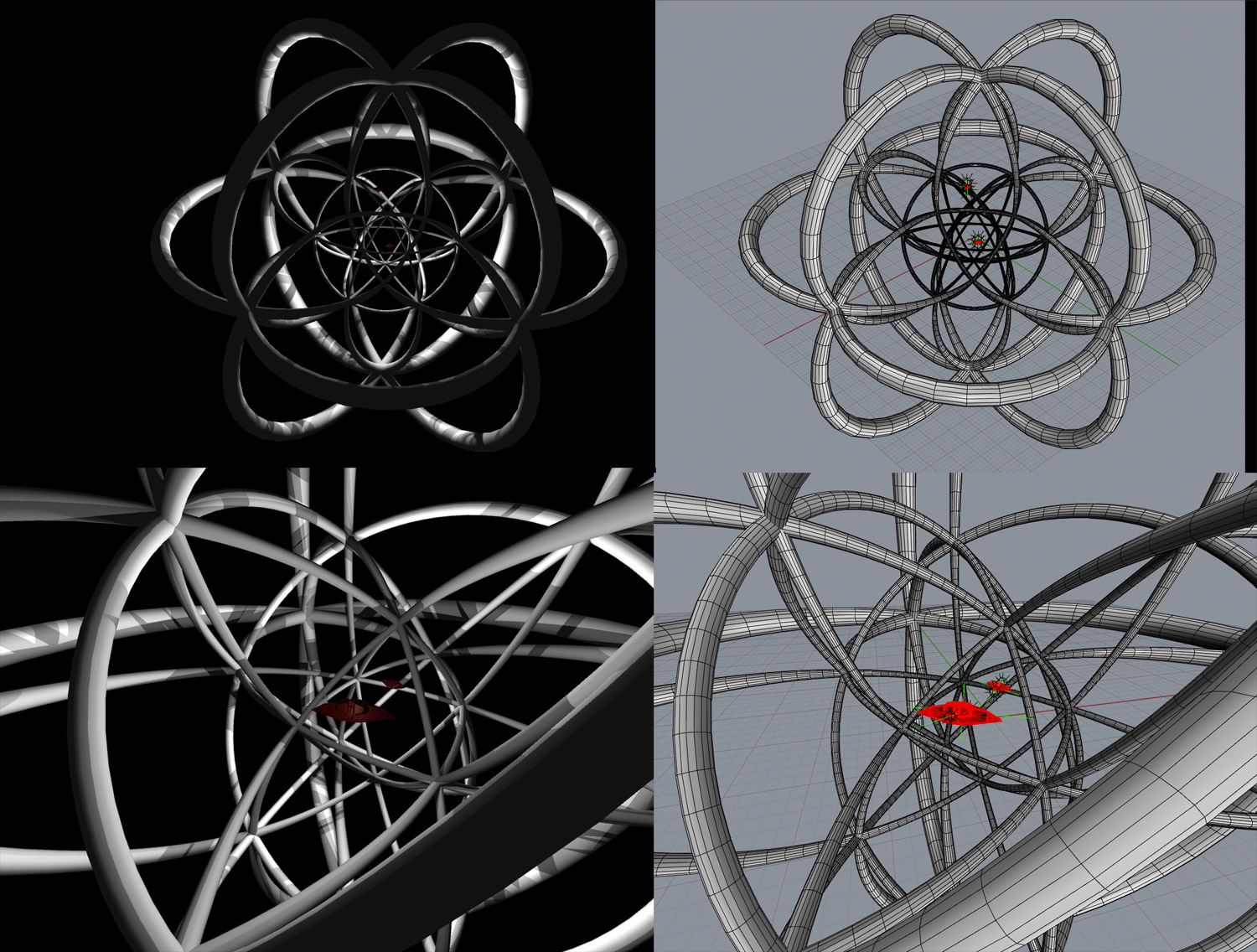
This is the hypercube, the 4-dimensional version of the cube. In 3D the cube is one of five regular polyhedra (the others being the tetrahedron, octahedron, dodecahedron and icosahedron, or in this crowd I suspect, the d4, d8, d12 and d20). In 4D there are 6 regular polytopes. Here are a couple of them, the 24-cell and the 120-cell:
WebGL rotatable model.
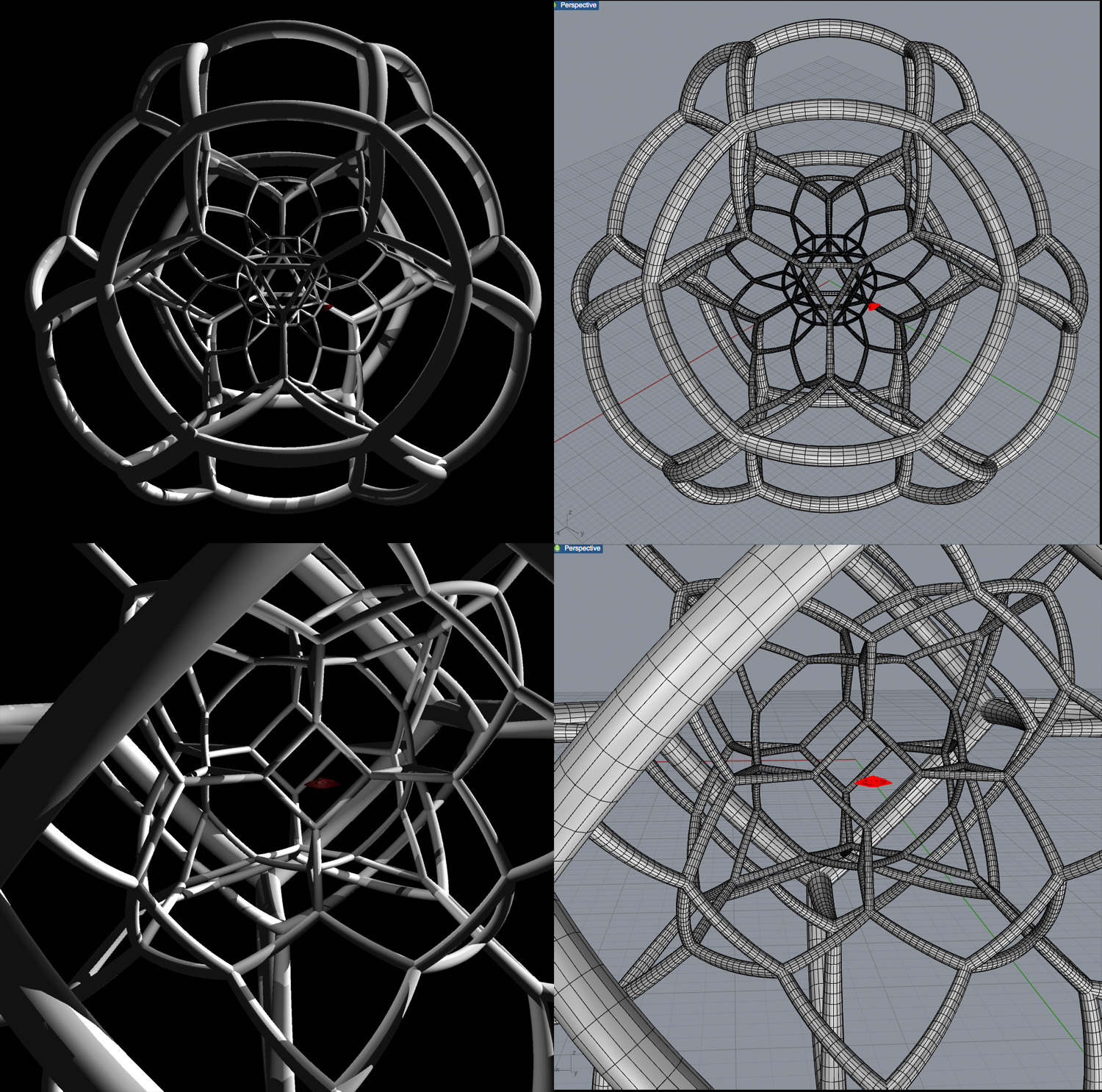
Here is the 120-cell, which as it's name suggests, has 120 dodecahedral cells:

WebGL rotatable model.
These might be good things to put wormholes or gates etc. at the center of.
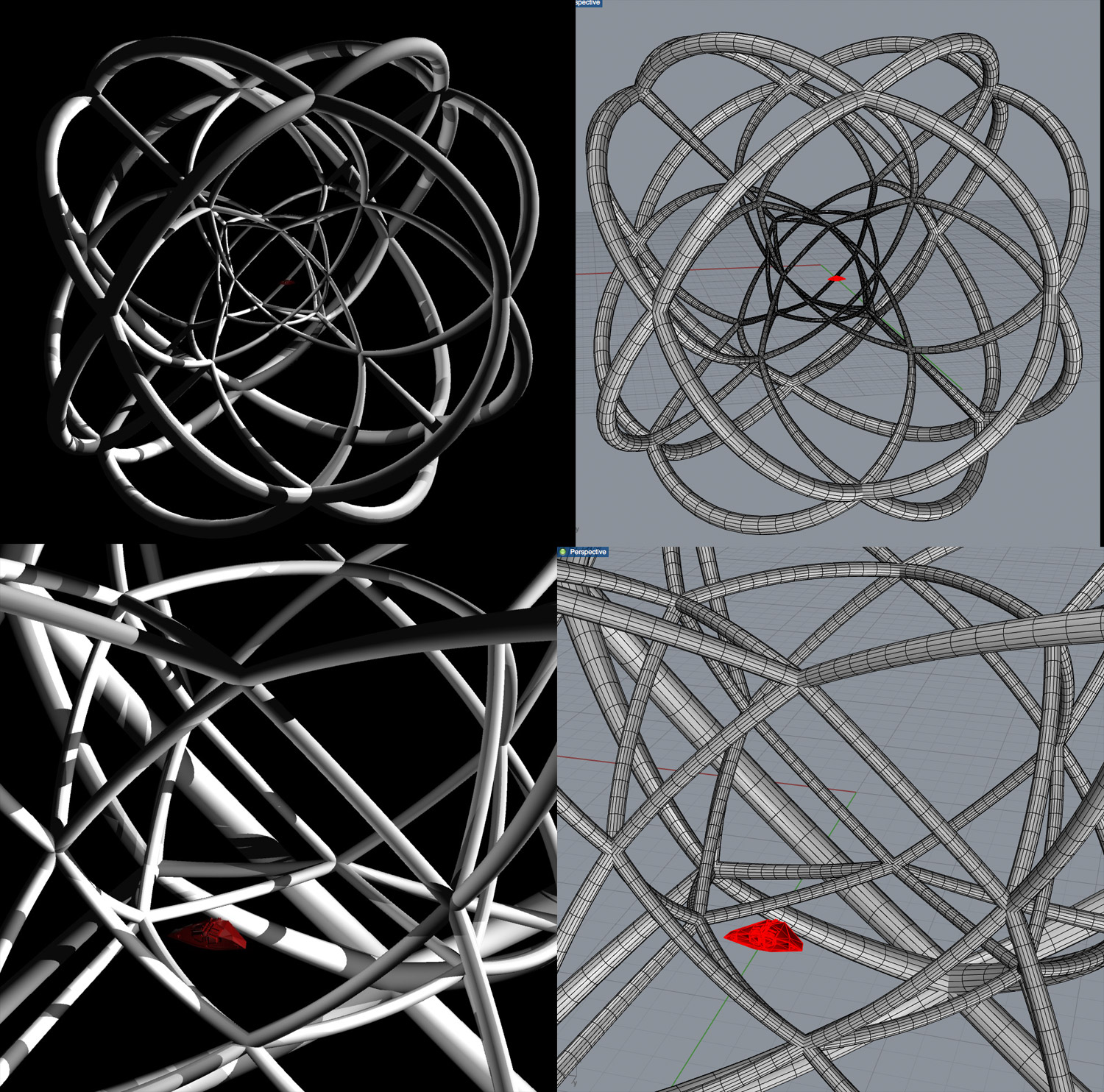
Finally, I had to figure out what the 4-dimensional version of the Coriolis station would be. The Coriolis station is in the shape of a cuboctahedron, which in some sense is half way between the cube and the octahedron. The 4-dimensional version of the cube is the hypercube, and the 4-dimensional version of the octahedron is the 16-cell, so the thing that is half way between those two is something called the "bitruncated tesseract":
WebGL rotatable model.
There is however an alternative, something called the "rectified tesseract". This has the advantage of having cuboctahedra inside it!
WebGL rotatable model.
Ok anyway, enough theory, what do these look like?

WebGL rotatable model.
This is the hypercube, the 4-dimensional version of the cube. In 3D the cube is one of five regular polyhedra (the others being the tetrahedron, octahedron, dodecahedron and icosahedron, or in this crowd I suspect, the d4, d8, d12 and d20). In 4D there are 6 regular polytopes. Here are a couple of them, the 24-cell and the 120-cell:

WebGL rotatable model.
Here is the 120-cell, which as it's name suggests, has 120 dodecahedral cells:

WebGL rotatable model.
These might be good things to put wormholes or gates etc. at the center of.
Finally, I had to figure out what the 4-dimensional version of the Coriolis station would be. The Coriolis station is in the shape of a cuboctahedron, which in some sense is half way between the cube and the octahedron. The 4-dimensional version of the cube is the hypercube, and the 4-dimensional version of the octahedron is the 16-cell, so the thing that is half way between those two is something called the "bitruncated tesseract":

WebGL rotatable model.
There is however an alternative, something called the "rectified tesseract". This has the advantage of having cuboctahedra inside it!

WebGL rotatable model.
