I'm pretty sure, that you can "see" the actual NS in this image, which I once made by stacking a few hundred different amateur photos of Messier 1. They were all captured in the visible wavelengths. It's the star roughly at the center of the image, below/right of the bright yellow star:
View attachment 147318
Of course, what you see is not the star, but emission and probably reflection from the surrounding gas.
Edit: Ok, with an apparent magnitude of 16.5 it's not the brightest star out there

If that star has Apparent Magnitude 16.5, and it is 6500 ly (1993 parsecs) away, and the web sources I found are accurate, and if I understood them, then its Absolute Magnitude is 5. Which just happens to be the same as Sol. So the Neutron star is putting out the same amount of light as Sol, but from a far smaller surface area.
So just to be clear, if our sun was replaced by that neutron star, then we would have the same light levels on Earth as we do currently, from an object about 10km across, 150 million kilometres away.
It is insanely bright, in the visible spectrum.
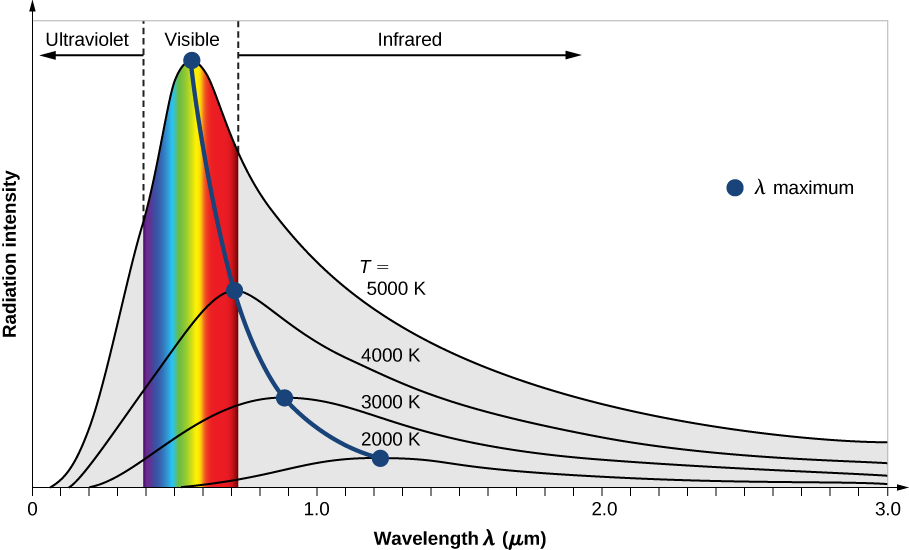
In the X-Ray spectrum, I'm less sure of my figures or what they mean, but I think if it follows a black-body curve, that gives it a peak at 3 angstroms (0.3nm) of about ten billion times more intensity. Is intensity a power thing or an amplitude thing?
It's fairly obvious that anything 270km from it would be fried by X-rays, but it's visible light we're interested in.
In my calculation above, the luminosity of the white dwarf was 0.0295
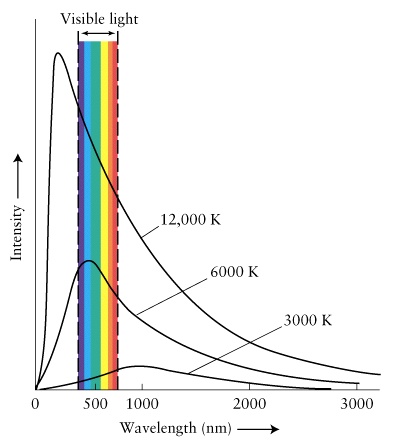
Sol has a luminosity of 1, centered in the visible spectrum.
So the M1 neutron star has an equivalent visible luminosity of 1, and it emits approximately 3.828E+26 watts in the visible spectrum.
And at a distance of 270km, that gives us 4E+14 watts per square metre at (waves hands) sort-of sun equivalent wavelengths.
In comparison, the incident power on Earth from the sun is 1360 watts per square metre.
That's such an outrageous answer that I checked the spreadsheet by putting in Earth's figures -- luminosity 1, distance 150Gm -- and got 1353 W/m2, which is close enough.
At 270km, neutron star M1 would be 300 billion times brighter than the sun is from Earth. That power would increase through the ultra-violet and into the x-rays until it reached a peak of a further ten billion times more intensity.
. In any case, I'm speaking solely of the visual spectrum, which is only a small slice of all that incident radiation. The image above showing the ships & large prominences looks more like what I would expect, bright but not so intense as to completely swamp any detail.