The choice of your coordinate system doesn't change the physical reality. You can turn and move it as you please. You could also use cartesian coordinates instead of spherical coordinates to navigate on a planet. That choice would have all sorts of impractical consequences unless you travel, in the polar areas...
How to navigate on a planet with the SRV
- Thread starter kilon
- Start date
Fair enough.
none of this helps with telling when to drop out of sc, at what distance and angle to get remotely close to a POI.
Which question?
I look forward to the day Flowy makes it to big school and realises this applies to him too now
I look forward to the day Flowy makes it to big school and realises this applies to him too now
And did I suggest I shouldn't be critizized or?
I look forward to the day Flowy makes it to big school and realises this applies to him too now
Hopefully finding it will be easier now.
Nope, sorry, again that's not the case. See the example I gave from the textbook. Also it doesn't actually fully make sense as a statement, as an angle, in of itself, is a directionless quantity.
Ermm, that's what the book says... in the angular motion section & relative to some frame an angle does have direction, it is in fact a way the direction is expressed when writing down vectors.
Also, I'm very sure that at least in math they are counted counter-clockwise, this is specially aparent when graphing the sine & cosine functions based from the unit circle which dictates their values from 0º to 360º.
Last edited:
Isn't that clockwise anyway? 90° on the right, 270° on the left.
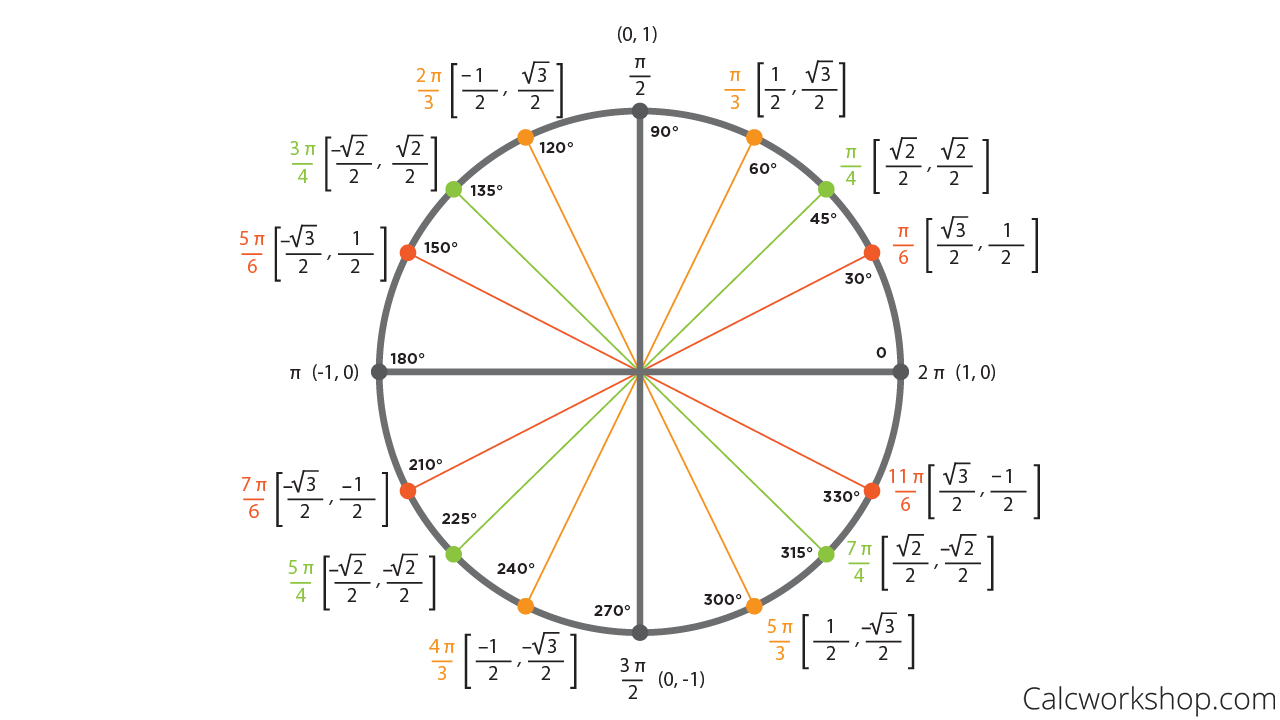
Look at the unit circle, 0º between the 1st & 4th cuadrant, then 90º is between the 1st & 2nd cuadrant & so on, it is definetly counter-clockwise.
Still seems to me that you have it the wrong way round. Clockwise is right-round (think steering wheel or handlebars), while counter-clockwise is left-round:
https://www.mathsisfun.com/geometry/clockwise-counterclockwise.html
SIt's a slightly different thing. When you're using a vector you're using a magnitude and a direction. You have to have a direction associated with the angle. The angle on it's own doesn't have a direction. Now, you can use a co-ordinate system in which the direction of the angles is pre-determined, but otherwise you need to specify it yourself.
For example, in Spherical Polar Co-ordinates, there's 3 co-ordinates (r, θ, Ф). r is the distance, Ф is the angle on the x-y plane (measured from the +ve x-axis in the direction of the +ve y-axis), θ is the angle from the +ve z-axis. (θ and Ф are sometimes swapped.)
A few key things here:
- θ is in no way measured clockwise or anti-clockwise, it is purely angle away from the +ve z-axis
- if you look directly down the z-axis, Ф appears to be measured in a counter-clockwise direction from the +ve x-axis
- if you look directly up the z-axis, Ф appears to be measured in a clockwise direction from the +ve x-axis
And on the Maths front let's take an example:
Let's define an abstract triangle, with sides A, B and C.
Is angle{A,B} different to angle{B,A}?
In my estimation, what's actually going on here is that a special case is being used for your course, but you're taking that special case to be the general case, which it isn't. - or to put it probably more accurately, you're being taught using a special case, but are not told that it's a special case, not a general case, and you've therefore got no way of knowing of your own accord that it's not the general case.
I hasten to add that there's nothing wrong with using a special case for teaching - it's often the only pragmatic thing to do, as the general case can often be much more difficult and it's better to equip students to use the special case, before building up to the general case. All understandable really!
Still seems to me that you have it the wrong way round. Clockwise is right-round (think steering wheel or handlebars), while counter-clockwise is left-round:
https://www.mathsisfun.com/geometry/clockwise-counterclockwise.html
Ermm, actually the source you provided shows that I'm right, if the unit circle where to to rotate clockwise, 90º would be between the 3rd & 4th cuadrant.
Preciesly, I said with reference to a frame.
I agree that in geometry angles don't have direction but that's simply because they have no use for it as you point out, in analytical geometry & in more abstract applications of angles like functions & calculus it is important to have an angle baseline & a direction, otherwise you'd not get consistant results for the trigonometric functions on which depends a whole lot of other theorems like e^([pi]*i)=-1.
For the unit circle, yes you are correct. But that's a special mathematical case. That doesn't apply to navigation in general. The unit circle is strange from a navigational perspective, as it places 0° on the left, and measures degrees counter-clockwise.
I hope you don't use the unit circle for navigating. Might not be harmful in Elite Dangerous, except you'll keep ending up at right angles to your intended destination. But you could get yourself and/or someone else hopelessly lost if you confuse the unit circle with a compass circle outside the game. As this thread is now showing an abundance of.
SFor the unit circle, yes you are correct. But that's a special mathematical case. That doesn't apply to navigation in general. The unit circle is strange from a navigational perspective, as it places 0° on the left, and measures degrees counter-clockwise.
I hope you don't use the unit circle for navigating. Might not be harmful in Elite Dangerous, except you'll keep ending up at right angles to your intended destination. But you could get yourself and/or someone else hopelessly lost if you confuse the unit circle with a compass circle. As this thread is now showing an abundance of.
Ermm, I preciesly said that I was talking about math, I made it clear that cartography was another story several times now.
Except this thread is about navigation on a planetary surface. So your math does not actually belong in this thread at all, regardless of how often you try to make the thread subject another story.
S